
|
Iztēles spēle |

papildināts 13.06.2005. |

|

Spēles būtība - uzvelc kādu nesakarīgu ķeburu un mēģini saskatīt, kas, galu galā, tur ir attēlots! Iesaisti citus šajā nodarbē, lai pārliecinātos, ka pat tad, kad Tev šķiet - citu variantu vairs būt nevar! - kāds ņems un ieraudzīs kaut ko pavisam pārsteidzošu!
Ķeburu drīkst grozīt visos virzienos, kā tik ienāk prātā. Zīmēt drīkst tikai ķebura kontūra iekšpusē.
...Zīmējumi... Ķeburs. Iesaku sagatavot ķeburu ~A6 formātā, otrā pusē paredzot vietu autora vārdam, citiem datiem, ja nepieciešams, un parakstam.
 |
 |
 "Es i īsts kovboj!" |
 "Iņ - jaņ sejas" |
 "Kurš fotografēja?" |
 "Kapteinis Nemo!" |
 "Augšā puļķīts, apakšā muļķīts" |
 "Bez paraksta" |
 "Vecmāmiņa" |
 "Lidot ir vislabāk!" |
 "Četrkājis" |
 "Monstrs" |
 "Bruņurupucis Bērtulis" |
 "Elviss FOREVER" |
 "Izbrīnītais ēzelītis" |
 "Lapa" |
 "Bez paraksta" |
 "Bez paraksta" |
 "Barons uz laukakmens" |
 "Ka tik nenokavēju!" |
 "Hei, kurš paņēma manu sniega lāpstu?" |
 "Bez paraksta" |
 "Bez paraksta" |
 "Jautrā radībiņa" |
 "Kuģa kapteinis - alnis bez ragiem" |
 "Zivs, kas atbaida ar savu slikto elpu" |
 "Turbosuns" |
 "Kā ar manu figūru???" |
 "Iešu, velšu sniega piku" |
 "Dobuma vērotāji" |
 "Arāba un kamieļa krustojums" |
 "Kas tas tāds?" |
 "Izbrīnītais putnēns" |
 "Arī raganas reizēm ir laipnas" |
 "M - ū - ū - ū - ū !" |
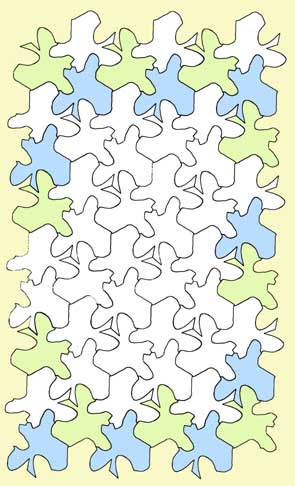
Visi šie zīmējumi var tikt savienoti kopīgā klājumā:
 |
 |
...Kas, kāpēc, no kā, par ko, ar ko, kā, kādā veidā... Kas.
Tik vienkārša spēle, bet tik plašas iespējas, ko tās sakarā varam uzzināt...
Kāpēc.
Ar to vaļasbrīžos var paniekoties gan lieli, gan mazi. Gan augsti skoloti, gan galīgi neskoloti. Gan veikli, gan neveikli. Gan kautrīgi, gan bezkauņas. VISI, kam nav slinkums mazliet paķēpāties...
Pastāstīt vēlos tāpēc, lai vēl kāds cilvēciņš piedzīvotu līdzīgus prieka mirkļus, kā ir gadījies man! :)
No kā.
Šīs spēles idejas ierosinātājs ir M.K.Eshērs (M.C.Escher), tāpēc būtu tikai vietā iepazīties ar šī interesantā cilvēka dzīvi un mākslu.
Ar šo materiālu varat iepazīties PowerPoint prezentācijā (~10Mb). Lai viegli un bez sāpēm izveidotu kādu ķeburu Eshēra stilā, kā arī uzreiz aplūkotu, kā izskatās ar izveidoto figūru noklāta plakne, var izmantot citu manis izveidotu jauku elektronisko līdzekli - t.i. MS Excel programmā izveidotu vidi "No četrstūra līdz ķeburam".
Laikam abas šīs datnes dabūt citādi nevarēs, kā rakstot man e-mailu un aprakstot savu vēlēšanos. Šādas vēlmes izpildīšu ātri, par citām varam parunāties... :)
Ieskats M.K.Eshēra darbos gūstams arī šādās mājas lapās:
- http://www.mcescher.com/
- http://home.comcast.net/~eschermc/
- http://www.worldofescher.com/
- Šajā lapā tiek īpaši analizēta M.K.Eshēra darba "Gleznu galerija" tehniskā izveide: http://escherdroste.math.leidenuniv.nl/
- Šeit var atrast diezgan plašu mākslinieka biogrāfiju un vēl dažus linkus tālākai izpētei: http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Escher.html
Materiāls sakārtots 7 daļās:
- M.K.Eshērs dzīvē un mākslā.
- Kā aizpildīt plakni ar vienādām figūrām?
- Ar kādiem daudzstūriem var noklāt plakni?
- Paralēlā pārnese un pagrieziens par leņķi.
- Konstrukcijas piemēri.
- Izmantotā literatūra.
- Tests.
2. daļā ar dažām animācijām (kuras gan nebūs redzamas vecākās PP versijās) mēģināju ilustrēt domu gaitu, kas palīdzētu katram pašam nonākt līdz idejām, kā radīt pašas vienkāršākās figūras, ar kurām iespējams pilnībā noklāt plakni vienā slānī.
3. daļā sīkāk tiek analizēts, kuri daudzstūri ir un kuri nav izmantojami plaknes noklāšanai. Tiek sniegts arī šo faktu pamatojums.
4. daļā jau pievēršamies sarežģītāku figūru iegūšanai. Izrādās, ka tas izdarāms izmantojot samērā primitīvas operācijas. Materiāls ilustrēts ar dažiem vienkāršiem piemēriem un animāciju.
5. daļā redzami piemēri no M.K. Eshēra mākslas darbiem. Patiesu izbrīnu rada tas, ka ar iepriekš aprakstītajām metodēm iespējams iegūt tik sarežģītas un reālas figūras!
Testā var pārbaudīt, vai kaut nedaudz esat sapratis šajā materiālā izklāstīto teoriju.
Par ko. Ar ko.
Šeit redzamie piemēri ir tapuši matemātikas vasaras nometnes laikā Mazsalacā, kad tās dalībnieki (5.-11.kl. skolēni) lika lietā savu iztēli un zīmēja savas idejas.
Tātad var secināt, ka šīs mākslas veidošanai nebūt nav nepieciešamas apzinātas māklinieka dotības (neapzinātas ir pilnīgi katram, neatkarīgi no tā, ko viņš pats par to domā!).
Kā, kādā veidā.
Manuprāt optimālais pasākuma plāns:
- Iepazīšanās ar M.K.Eshēra dzīvi un mākslu, kā arī ar dažām iespējām, kā katrs pats var izveidot Eshēra tipa zīmējumus.
- Katrs atsevišķi vai visi kopā mēgina izveidot kādu interesantu figūru, ar kuru var noklāt plakni.
Kādu figūru kopīgi izvēlas tālākajai iztēles spēlei. - Uz nelielām lapiņām (A6 formātā), uz kurām sakopēts minētajā veidā radītais ķeburs, katrs zīmē savas idejas. No sirds iesaku katram zīmējumam pievienot parakstu, jo dažreiz tikai paraksts spēj atklāt uzzīmētā patieso un ģeniālo būtību!
- Var sarīkot konkursu par interesantāko zīmējumu un izstādi. Interesanti būs paskatīties visus darbiņus kopā!

|
|
|