Initialization
In[49]:=
Out[49]=
In[1]:=
In[8]:=
In[11]:=
In[13]:=
In[16]:=
In[17]:=
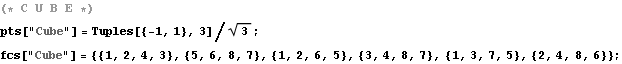
In[19]:=
In[20]:=
In[21]:=
1. Constructions in 
1.1. Regular simplex in 
embeded into 
The simplest way to obtain the coordinates of n+1 vertices of a regular simplex in 
is to embed it into 
. Then the coordinates of the vertices are the cyclic permutations of 
.
In[22]:=
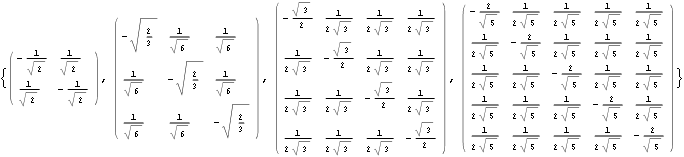
1.2. Recursive construction of a regular simplex
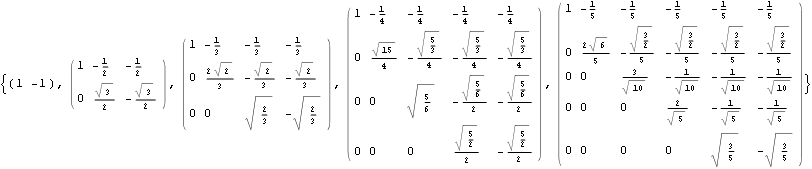
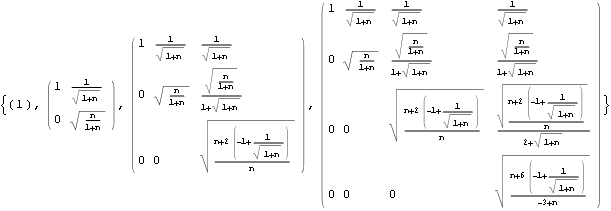
There is a recursive way to construct a regular simplex that is centered at the origin and inscribed in a unit sphere. For example, regular simplex in 1 dimension is just a line segment from -1 to 1. To construct a regular triangle, we take this line segment and just add a new point in the 2nd dimension. However, we must do some additional operations if we want the obtained simplex to be centered at the origin and inscribed in a unit sphere. For example, to construct a tetrahedron, we take a regular triangle in the xy-plane, scale it down by a certain amount, then push it down by a certain amount along z axis and finally add a new point on z axis with z coordinate equal to 1. In general we rescale the previous simplex by factor 
and push it down by amount 
.
In[23]:=
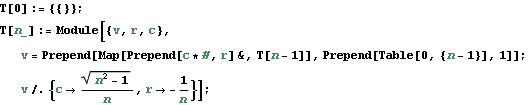
1.3. Construction in the non-negative orthant
This is a construction of n vectors in the non-negative orthant of 
, sucht that the inner product between any two of them is 
. Sometimes this set of vectors can be extended to a SIC-POVM. The construction works as follows. The first vector we take to be 
. Then the next must be 
, where 
and 
. The third vector we take to be of the form 
, where 
and 
. Next we take 
and so on. Notice that each time only two components of the previous vector must be modified - the penultimate component must be modified to get the right inner product with the previous vector and the last component must be modified to normalize the vector. Probably it is possible to find a simpler construction that achieves the same result. For dimensions n=2, n=3, n=4 it is possible to extend this set of vectors to a complete SIC-POVM (see Section 2.1., 3.2., 4.1.). However, numerical experiments suggest that it is not possible for n=5.
In[25]:=
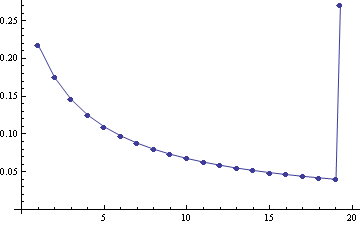
For n=20 the components of the last vector 
are distributed as follows.
In[46]:=
Out[46]=
2. SIC-POVMs for n=2
2.1. The simplest construction
The simplest possible SIC-POVM. Without loss of generality we can take the first vector to be 
. Thus the first component of the remaining vectors must have absolute value 
. Without loss of generality we can take it to be exactly 
, since we can ignore the global phase of each vector. Thus the second component of the remaining vectors must have absolute value 
. Since we can multiply the i-th row by any phase, we can choose the second component of the second vector to be exactly 
. The second component of the remaining vectors is obtained by adding an appropriate phase to 
. Note that the first two vectors coincide with those obtained using non-negative orthant construction.
In[32]:=
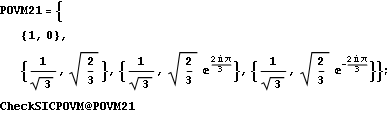
Out[33]=
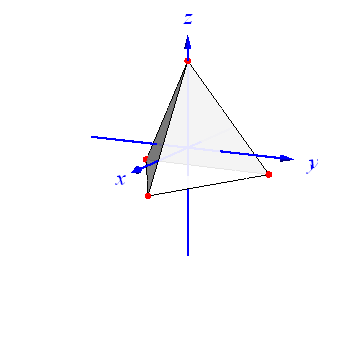
The Bloch vectors corresponding to these states are the vertices of a regular tetrahedron whose one face is parallel to xy-plane. The pairwise inner product of the Bloch vectors is 
.
2.2. Taking 4 vertices of a cube
Here is another construction of SIC-POVM in two dimensions.
In[34]:=
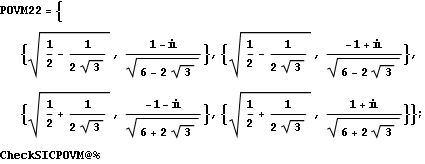
Out[35]=
This time the tetrahedron is obtained by taking 4 vertices of a cube, such that no two are adjacent. The coordinates of the vertices of a cube that is centered at the origin and inscribed in a unit sphere is 
.
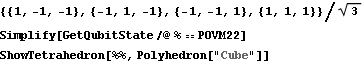
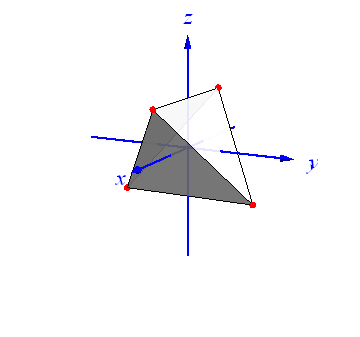
2.3. Tetrahedron with 2 edges parallel to coordinate axes
This SIC-POVM is obtained from another construction of a tetrahedron in 3 real dimensions.
In[36]:=
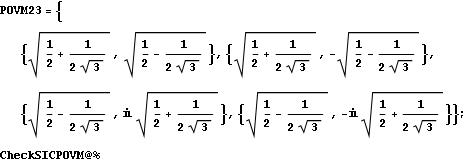
Out[37]=
In this case two edges of the tetrahedron are parallel to the x and y axes respectively.
3. SIC-POVMs for n=3
3.1. Extending SIC-POVM for n=2
This SIC-POVM is obtained from the first SIC-POVM in 2 dimensions described in Section 2.1. The idea is similar to that used to construct a tetrahedron in 3 dimensions from a regular triangle in 2 dimensions described in Section 1.2.
In[38]:=
Out[39]=
Note that the first vector from the first row together with three vectors from any of the remaining rows resemble the SIC-POVM described in Section 2.1.
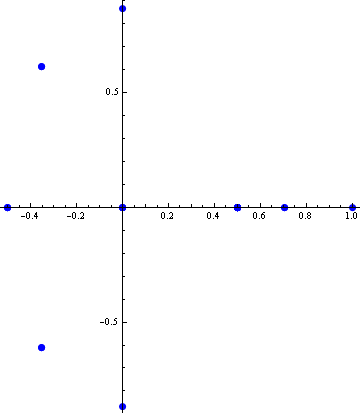
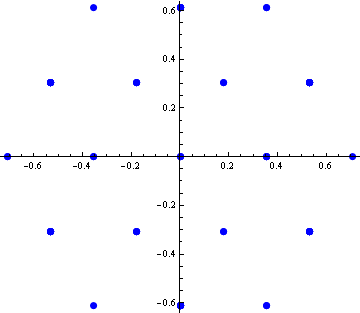
If we take all components of all vectors and plot them in the complex plane, we get the following picture.
For each triple of vectors from the SIC-POVM we can make a matrix whose columns consist of the chosen vectors. Then we can compute the determinants of all these matrices and plot the obtained complex number in the complex plane. The resulting picture looks as follows.
Compute the gram matrix and plot its entries in the complex plane.
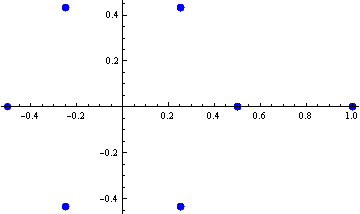
3.2. Non-negative orthant construction
This SIC-POVM is obtained by extending the set of vectors obtained from the construction in the non-negative orthant described in Section 1.3.
In[40]:=
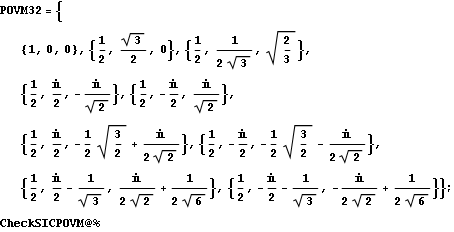
Out[41]=
If we take all components of all vectors and plot them in the complex plane, we get the following picture.
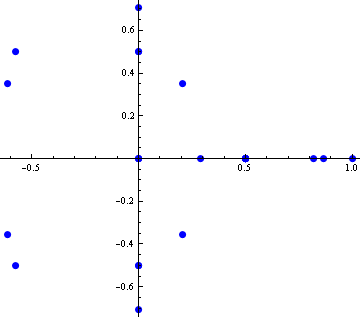
For each triple of vectors from the SIC-POVM we can make a matrix whose columns consist of the chosen vectors. Then we can compute the determinants of all these matrices and plot the obtained complex number in the complex plane. The resulting picture looks as follows.
Compute the gram matrix and plot its entries in the complex plane.
4. SIC-POVMs for n=4
4.1. Non-negative orthant construction
The columns of the following matrix correspond to the vectors that form the SIC-POVM. The first four vectors of this SIC-POVM are obtained from the construction in the non-negative orthant described in Section 1.3.
In[42]:=
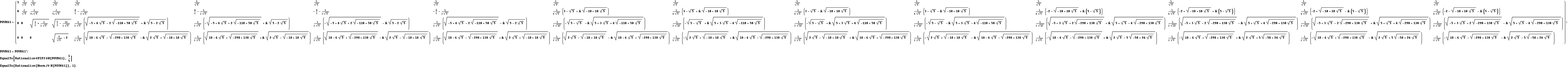
Out[44]=
Out[45]=
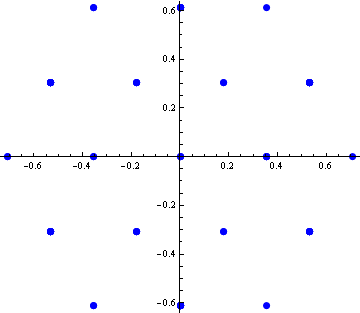
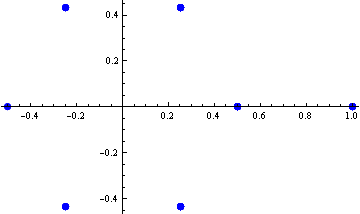
If we take all components of all vectors and plot them in the complex plane, we get the following picture (some points lie on circles).
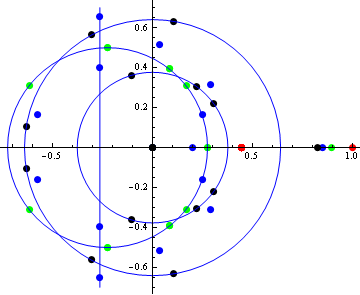
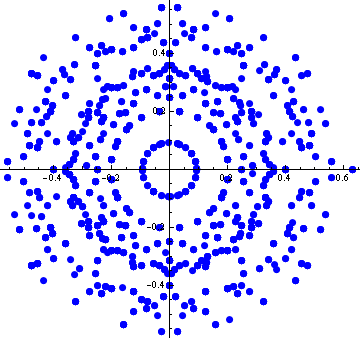
For each quadruple of vectors from the SIC-POVM we can make a matrix whose columns consist of the chosen vectors. Then we can compute the determinants of all these matrices and plot the obtained complex number in the complex plane. The resulting picture looks as follows.
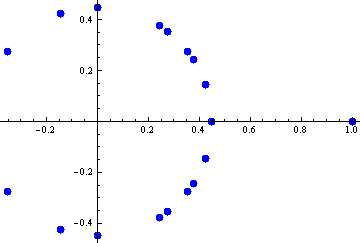
Compute the gram matrix and plot its entries in the complex plane.
There are only 18 disctinct elements in the gram matrix.
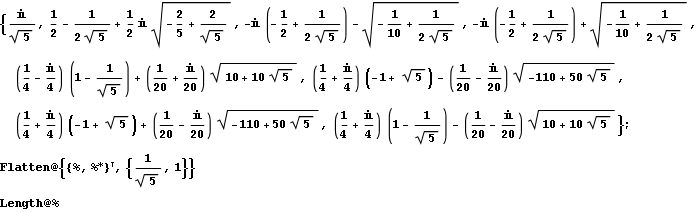
5. Constructions in 
5.1. First three elements of any SIC-POVM
We can apply a unitary transformation to the given SIC-POVM so that the first vector becomes 
. Then the first component of the remaining vectors can be taken equal to 
, since we can ignore the global phase for each vector. The second component of the second vector can be taken equal to 
, since we can multiply the i-th component of each vector by the same phase without affecting the inner products. Hence we can always transform our SIC-POVM so that the second vector becomes 
. Finally, the third vector is of the form 
for some α=x+i y and β. The absolute value of the inner product of the 2nd and 3rd vectors gives us conditions for x and y.
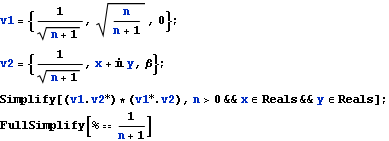
This is an equation of a circle with center 
and radius 
. Hence any SIC-POVM can be transformed so that the first three vectors become:
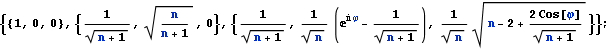
5.2. Zero in the 3rd component
Observe that the first three vectors of the SIC-POVM described in Section 3.1. have the 3rd component equal to 0. One might ask if this could happen in higher dimensions too. Unfortunately the answer is no.
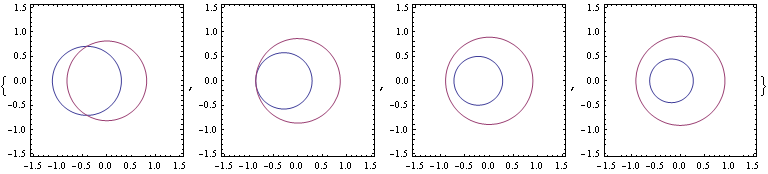
Both conditions can be satisfied simultaneously only if there is a point common to both circles. This happens only when n=2 or n = 3.
