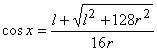Studentiem

Fizikas un matemātikas fakultāte

Matemātikas maģistra programma

Ekstrēmu uzdevumu risināšanas elementārās metodes

Autors                          LU asoc. prof. A. Cibulis

Kursa apjoms               4 kred. p.

Pārbaudes forma          eksāmens

Priekšnosacījumi           vispārējā matemātiskā sagatavotība bak. programmas apjomā

Kursa kods                  Mate-

Anotācija

Kursā aplūkotas elementārās ekstrēmu uzdevumu risināšanas metodes. Analizētas vairākas funkciju klases. Sniegta vēsturiska informācija, kā arī jauni rezultāti.

Saturs

1.      Ievads. Slavenību vārdā nosaukti ekstrēmu uzdevumi (Eiklīda, Hērona, Tartaļjas, Zēnodora, Heigensa, Šteinera u. c. uzd.).

2.      Piemēri no dabas, kur realizējas kāds no optimalitātes principiem.

3.      Ekstrēmu teorijas jēdzieni un to apspriešana. Matemātisko modeļu sastādīšana.

4.      Ekstrēmu uzdevumu risināšanas elementārās metodes un paņēmieni. Dažādu nevienādību lietošana (nevienādības starp aritmētisko, ģeometrisko, kvadrātisko u. c. vidējiem lielumiem; Košī, Jensena, Čebiševa u. c. nevienādības). Vērtību kopas izmantošana. Monotonitātes izmantošana. Ģeometriskas interpretācijas lietošana.

5.      Funkciju klases (kvadrātfunkcija, kubiska funkcija, polinomi, trigonometriskas u. c. funkcijas)

6.      Diskrētie ekstrēmu uzdevumi.

7.      Ekstrēmu uzdevumi matemātikas olimpiādēs.

8.      Sofismi par ekstrēmu uzdevumiem.

9.      Īss ieskats ekstrēmu uzdevumu klasiskās neelementārās risināšanas metodēs.

Prasības kredīta iegūšanai

Prast definēt attiecīgos jēdzienus, risināt uzdevumus un sastādīt matemātiskos modeļus.

Literatūra

1. Cibulis A. Ekstrēmu uzdevumi 1. daļa. - Rīga, “Mācību grāmata”, 2003, 104 lpp.

2. Cibulis A. Ekstrēmu uzdevumi 1.-5. daļa, (http://www.liis.lv/).

3. Niven I. Maxima and Minima Without Calculus,  

    Dolciani  Mathematical Expositions, Math. Assoc. of America , No. 6, 1981.

4.Boзняк Г.M.,Гуceв B.A. Прикладаныe задачи на экcтрeмумы,

  М.,Просвещение,1985,144 с.

5.Зетель С.И. Задачи на максимум и минимум,

  М.-Л.,Гостехиздат,1948,224 c.

6.Крыжановский Д.А. Изопериметры,Физматгиз,1959,116 с.

7.Тихомиров В. М. Рассказы о максимумах и минимумах,

  М.,Наука,1986,190 с.

8.Харди Г.Г.,Литллвуд Д.Е.,Полиа Г. Неравенства,

  М.,ИЛ,1948 (1932),456 с.

9.Шклярский Д.О.,Ченцов Н.Н.,Яглом И.М. Геомерические

  неравенства,и задачи на максимум и инимум,М.,Наука,1970,335 с.

10. Herman J., Kučera R., Šimša J. Equations and inequalities. Elementary problems and theorems in algebra and number theory, CMS, New York: Springer-Verlag, 2000, 344 pp.

Elementary methods for  solving extremum problems

Annotation
Elementary methods for solving extremum problems have been dealt with in this
course. Several classes of functions have been analysed. Historic information has been given and new findings have been set forth as well.

1. d.  (Heigensa uzdevums 2 un 3 lodītēm)

Ja lode L_M ar masu M un ātrumu V ietriecas nekustīgā lodē L ar masu m, tad pēdējā iegūst ātrumu . Izrādās, ka novietojot starp šīm divām lodēm trešo lodi, var panākt lielāku (nekā v) pēdējās lodes L ātrumu. Kāda jāņem trešās lodes masa m₁, lai lode L iegūtu maksimālo ātrumu? Vispārīgā gadījumā jānoskaidro, kādas jāņem n ložu masas m < m₁ < m₂ < ….< m _n < M, lai pēc to secīgām sadursmēm pēdējā lode L iegūtu maksimālo ātrumu? Atrisināt Heigensa uzdevumu, ja  n = 2 un n = 3.

Piezīme. Uzdevuma elementārs risinājums vienas starplodītes gadījumā atrodams [1]. Konspektīvs Heigensa uzdevuma risinājums ar diferenciālrēķinu palīdzību dots grāmatā

Зорич В.А. Математический анализ часть 1,Москва,Наука,1981,544c.

2. darbs (Optimālais paralēlskaldnis)

Uzdevums. No visiem taisnstūra paralēlskaldņiem ar uzdotu pamata laukumu L un sānu virsmas laukumu S atrast to, kuram šķautņu garumu summa ir vismazākā. Vai optimālais paralēlskaldnis būs kubs?

3. darbs (Pierādīt teorēmu)

Teorēma. Pieņem, ka funkcijas f  =  definīcijas kopa D(f) ir nogrieznis [m, M]  ar galapunktiem , ac < 0.

Tad funkcija f sasniedz minimumu punktā m, ja a + c > 0 un punktā M, ja a + c < 0. Ja turklāt  , tad 

.

4. darbs (Piala, trigonometriska funkcija)

Nekustīgi nostiprinātā tasītē – puslodē, ar rādiusu r ievieto homogēnu stieni ar garumu l, 2r < l < 4r. Atrast stieņa līdzsvara stāvokli. Līdzsvara stāvoklis raksturojas ar minimālo potenciālo enerģiju, t. i., no visiem pieļaujamiem stāvokļiem stieņa smaguma centram jāatrodas viszemāk. Kādai attiecībai jāpastāv starp r un l, lai leņķis x starp puslodes diametru un stieni līdzsvara stāvoklī būtu 1) 60⁰;  2) 45⁰?

Minimizējamā funkcija .

Minimuma punkts

5. darbs (izliektība)

            Pierādīt funkcijas

,

izliektību vai ieliektību.